help("dpois")
dpois(3,0.75)[1] 0.03321327ppois(2,0.75)[1] 0.9594946Lab 7 - with solutions
Please note that there is a file on Canvas called Getting started with R which may be of some use. This provides details of setting up R and Rstudio on your own computer as well as providing an overview of inputting and importing various data files into R. This should mainly serve as a reminder.
Recall that we can clear the environment using rm(list=ls()) It is advisable to do this before attempting new questions if confusion may arise with variable names etc.
Example 1
In this example we let \(X\sim \text{Po}(0.75)\) and we calculate \(P(X=3)\) and \(P(X\leq 2)\), and we will plot this distribution.
- Input the code below to calculate the probabilities. Note the help functions that are useful for determining the arguments.
- For the plot we will create a sequence of 15 numbers, calculate the corresponding probability mass function and the plot these against each other.
x<-seq(0,14, length=15)
dx<-dpois(x,0.75)
plot(x,dx, xlab="x value",type="p", ylab="Probability", main="Poisson(0.75) Distribution")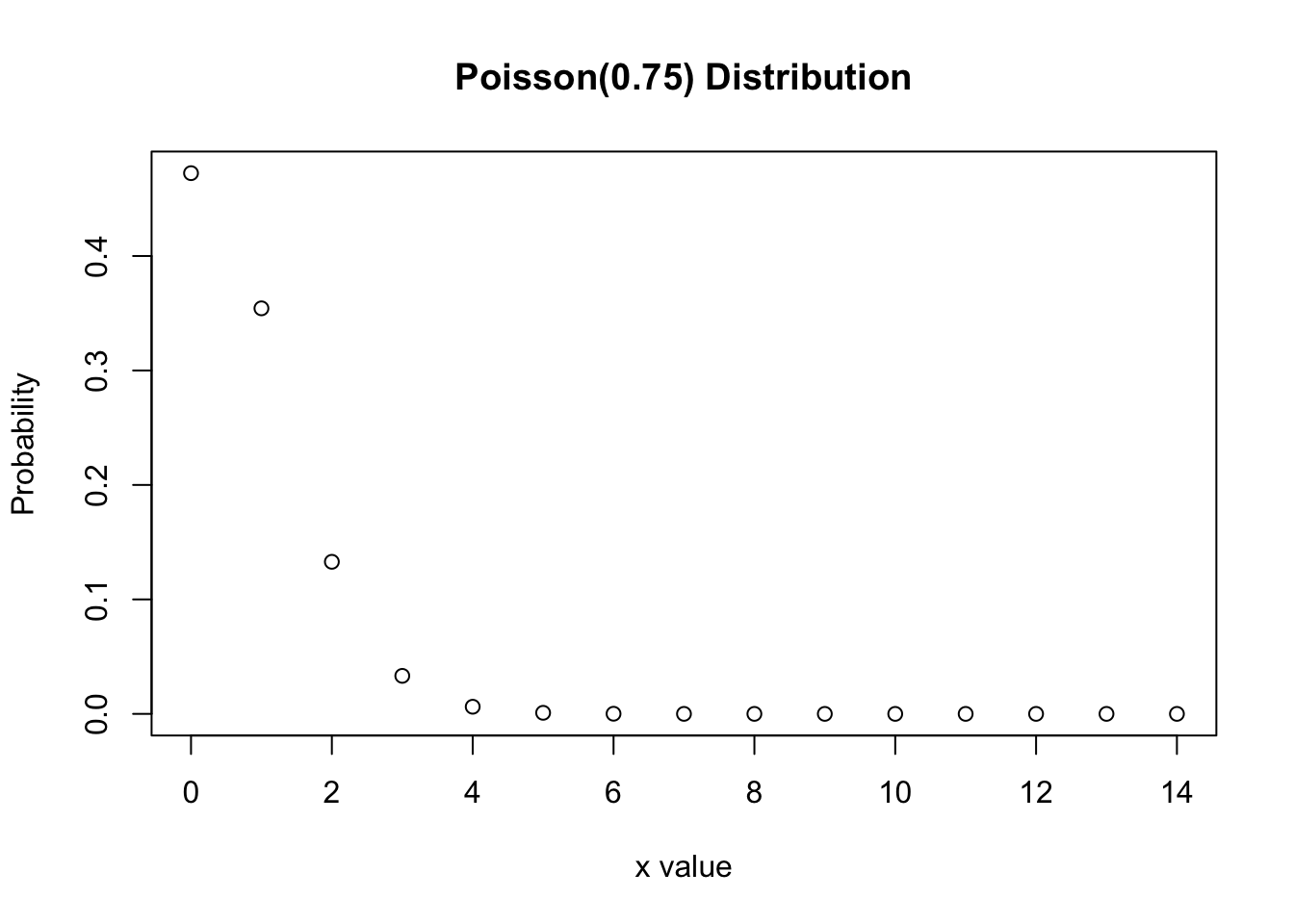
Exercise 1
For \(Y\sim Po(1.5)\) find \(P(Y=1)\) and \(P(Y>3)\).
Solution
- \(P(Y=1):\)
dpois(1,1.5)[1] 0.3346952- \(P(Y>3):\)
ppois(3,1.5, lower.tail=F)[1] 0.06564245Example 2
In this example we will create Poisson random numbers and then test to see whether the numbers generated follow a Poisson distribution.
Note: Everyone’s results will likely be different as this is a random process.
- Firstly, let’s create and view a random sample of size 20 from a \(Po(2.5)\) distribution.
help("rpois")
RandomSample<-rpois(20,2.5)
RandomSample [1] 2 4 1 1 3 1 7 2 3 5 3 8 3 2 4 0 2 5 2 1- Next we consider the mean, variance and a visualisation of the sample:
mean(RandomSample)[1] 2.95var(RandomSample)[1] 4.260526hist(RandomSample)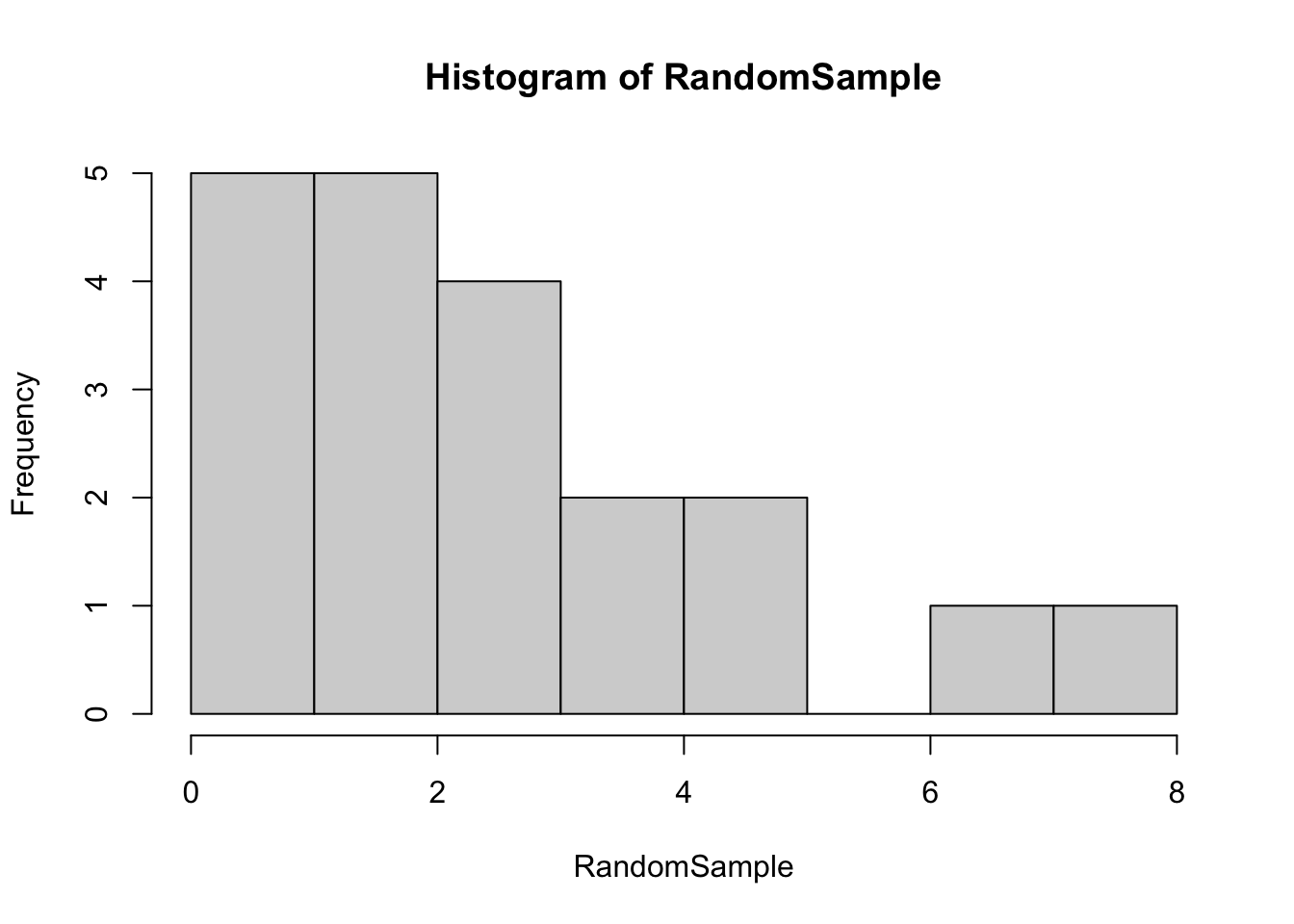
Exercise 2
Repeat the example above, but change the mean of the Poisson distribution that you initially generate random numbers from.
Solution
This will depend on your individual choice of the mean of the distribution (and the randomness of the procedure).
Example 3
This example considers creating a log-linear model for count data, i.e. Poisson regression. In the lectures, estimates of the parameters were just stated; now we will use R to obtain these. We will see the full details of the Surgery example and investigate whether Number of Surgery Visits is related to Location via a log-linear model. We assume a Poisson distributed dependent variable and independence.
- We first import the dataset and check it using the code below:
library(foreign)
Surgery<-read.spss(file.choose(), to.data.frame = T)head(Surgery) Patient Location SurgeryVisits
1 1 0 1
2 2 0 2
3 3 1 5
4 4 1 6
5 5 1 5
6 6 0 1- Next we perform the log-linear/Poisson regression analysis
SurgeryPoissonReg<-glm(SurgeryVisits~factor(Location), data=Surgery, family="poisson")
summary(SurgeryPoissonReg)
Call:
glm(formula = SurgeryVisits ~ factor(Location), family = "poisson",
data = Surgery)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.4138 -0.3379 -0.2238 0.1303 2.0000
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.8473 0.2673 3.170 0.00152 **
factor(Location)1 0.7033 0.3190 2.205 0.02745 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 14.1586 on 12 degrees of freedom
Residual deviance: 8.9034 on 11 degrees of freedom
AIC: 52.038
Number of Fisher Scoring iterations: 5- You should obtain the following output:
- To help us evaluate the model we can use the following code which provides a \(p-\)value for the Deviance statistic and Wald chi-square statistics:
anova(SurgeryPoissonReg, test="Chisq")Analysis of Deviance Table
Model: poisson, link: log
Response: SurgeryVisits
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev Pr(>Chi)
NULL 12 14.1586
factor(Location) 1 5.2551 11 8.9034 0.02188 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- The Residual deviance/df\(=\tfrac{8.9034}{11}=0.81\) is close to 1, (and the corresponding p-value is \(0.02188<0.05\)) indicating a good model fit.
install.packages("lmtest")library(lmtest)
help("waldtest")
waldtest(SurgeryPoissonReg, test="Chisq")Wald test
Model 1: SurgeryVisits ~ factor(Location)
Model 2: SurgeryVisits ~ 1
Res.Df Df Chisq Pr(>Chisq)
1 11
2 12 -1 4.8621 0.02745 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The Wald Chi-Square statistic is significant for Location (p-value of \(0.027<0.05\)) indicating the significance of the Location variable.
Further, from the earlier output, note that \(\hat{b}_0=0.847\); and \(\hat{b}_1=0.703\), i.e. we have the model, \[ \ln \hat{\lambda}_i=0.847+0.703x_{i1}, \text{ or } \hat{\lambda}_i=e^{0.847+0.703x_{i1}}=e^{0.847}(e^{0.703})^{x_{i1}}. \]
Exercise 3
The Poisson Log-linear (PCP Defaults) dataset contains the number of defaults on personal contract plans (PCPs) for a certain car dealership according to their customers’ salary band. The Salary variable has 3 categories, 0, 1 and 2. Create a Poisson log-linear model for these data. You may assume independence and that the dependent variable is Poisson distributed. Make sure you analyse the output.
Hint: In this question the categorical variable (Salary) has more than 2 categories - this makes interpreting the model more complicated. The notes on dummy variables in the lecture notes should help you, along with Example 3 on the R examples class sheet.
Solution
- We first import and check the dataset.
library(foreign)
PCP<-read.spss(file.choose(), to.data.frame = T)head(PCP) Customer Salary DefaultNumber
1 1 0 5
2 2 0 6
3 3 1 3
4 4 2 3
5 5 2 5
6 6 1 4attach(PCP)- We now perfom the loglinear/Poisson regression analysis.
PCPReg<-glm(DefaultNumber~factor(Salary), data=PCP, family="poisson")
summary(PCPReg)
Call:
glm(formula = DefaultNumber ~ factor(Salary), family = "poisson",
data = PCP)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.1213 -0.2583 0.0000 0.1671 1.5764
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.7228 0.1890 9.116 <2e-16 ***
factor(Salary)1 -0.6242 0.3200 -1.951 0.0511 .
factor(Salary)2 -0.9118 0.3832 -2.380 0.0173 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 16.5487 on 13 degrees of freedom
Residual deviance: 8.9861 on 11 degrees of freedom
AIC: 56.247
Number of Fisher Scoring iterations: 5- In order to evaluate the model (Deviance and Wald chi-square statistics) we use the following code:
anova(PCPReg, test="Chisq")Analysis of Deviance Table
Model: poisson, link: log
Response: DefaultNumber
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev Pr(>Chi)
NULL 13 16.5487
factor(Salary) 2 7.5627 11 8.9861 0.02279 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1install.packages("lmtest")library(lmtest)
waldtest(PCPReg, test="Chisq")Wald test
Model 1: DefaultNumber ~ factor(Salary)
Model 2: DefaultNumber ~ 1
Res.Df Df Chisq Pr(>Chisq)
1 11
2 13 -2 7.3907 0.02484 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Analysis of the output:
The deviance/df is 0.817, indicating a good model fit. Furthermore, the Wald chi-square statistic is significant indicating the significance of the Salary variable.
The three categorical variables are combined into 2 dummy variables, say \(d_1\) and \(d_2\), where \(d_1\) and \(d_2\) take the values \(0\) or \(1\), i.e. we have a model of the form: \[ y_i=e^{b_0+c_{1}d_{1}+c_{2}d_{2}}. \]
In particular, we have: \[ y_i=e^{1.723-0.912d_{1}-0.624d_{2}}. \]
The base case is where \(d_1=d_2=0\), and this corresponds to salary band \(0\) in this case. Therefore, for salary band 0, we have, \[ y_i=e^{1.723}=5.6, \quad \text{i.e. 5.6 defaults for people in band $0$.} \]
Another possibility is when \(d_1=1\) and \(d_2=0\), and this corresponds to salary band \(2\). In this case the model is, \[ y_i=e^{1.723-0.912\times1-0.624\times 0}=2.25, \quad \text{i.e. 2.25 defaults for people in band $2$.} \]
Finally, for \(d_1=0\) and \(d_2=1\), i.e. for salary band \(1\), we have, \[ y_i=e^{1.723-0.912\times0-0.624\times 1}=3, \quad \text{i.e. 3 defaults for people in band $1$.} \]